Title: Dual-Triangular QR Decomposition with Global Acceleration and Partially Q-Rotation Skipping

Reference:

1. Tall and Skinny QR factorizations in MapReduce architectures

2. Dataflow Systolic Array Implementations of Exploring Dual-Triangular Structure in QR Decomposition Using High-Level Synthesis （HLS version of this article）

My implementation: my_repo

Intro

QR分解在边缘计算, 数据压缩, 降维, 还有特征值计算等方面有着广泛的应用场景，一方面是他的算法并行性很好，比如givens变换一次只对一行数据处理，可以同时处理多行，另一方面是它的数值稳定性好。

在流媒体等边缘任务中，我们遇到的大多是Tall and Skinny Matrix，比如视频中一秒有60帧，但一帧却有百万像素。在这样的矩阵上做QR分解，目标则是把m×n matrix A (m > n)分解成m×n matrix Q with orthogonal columns和n × n upper triangular matrix R。从数学理论上来说，这么分解是可以的，相当于在$R^n$中的m维子空间，m个基组成Q，其余的完全照搬Schmidt正交化，而且相应的数值方法（包括Householder和Givens变换，Schmidt方法）一定也是可以使用的。

但是，如果直接强行做整个Householder或Givens变换，会在边缘平台（FPGA）上带来很大的计算和存储负担，并且也不能很好的并行化，存在大量的同步开销。很自然的，对待这样一个行列数不成正比的矩阵，我们有这样一个最初的并行工作流（communication avoiding QR, CAQR）：先将m分成多个n，然后一一分解，最后再组合起来，此时Q并不是显式表示的，而是由一系列矩阵之积表示。

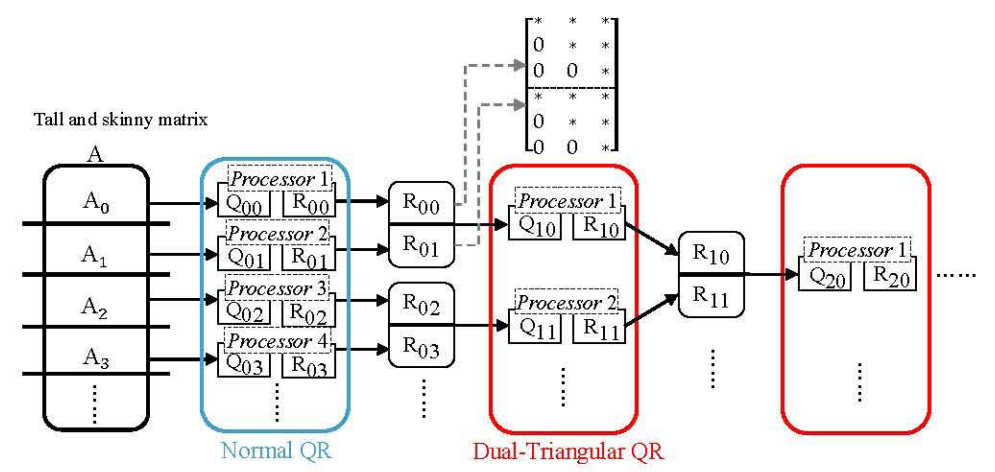
可以发现分解算法由两个基本操作组成：Normal QR和Dual-triangular QR (DTQR)。普通QR已经被很深入的研究过 ，但是DTQR却没有怎么利用他的双三角结构，而是直接用普通QR代替。这一篇文章则是针对这方面做出了优化，采用并行Givens变换来加速计算（Householder是串行算法，是对整个矩阵运行，而Givens一次只计算两行，可以大量并行）。

PS: 还有的文章[1]则是在任务级做出优化，将上面的数据流并行化，在MapReduce上计算。它实现了mapper（串行块），reducer（多个并行的串行块的缩并），scheduler（根据不同串行块情况分配缩并组）

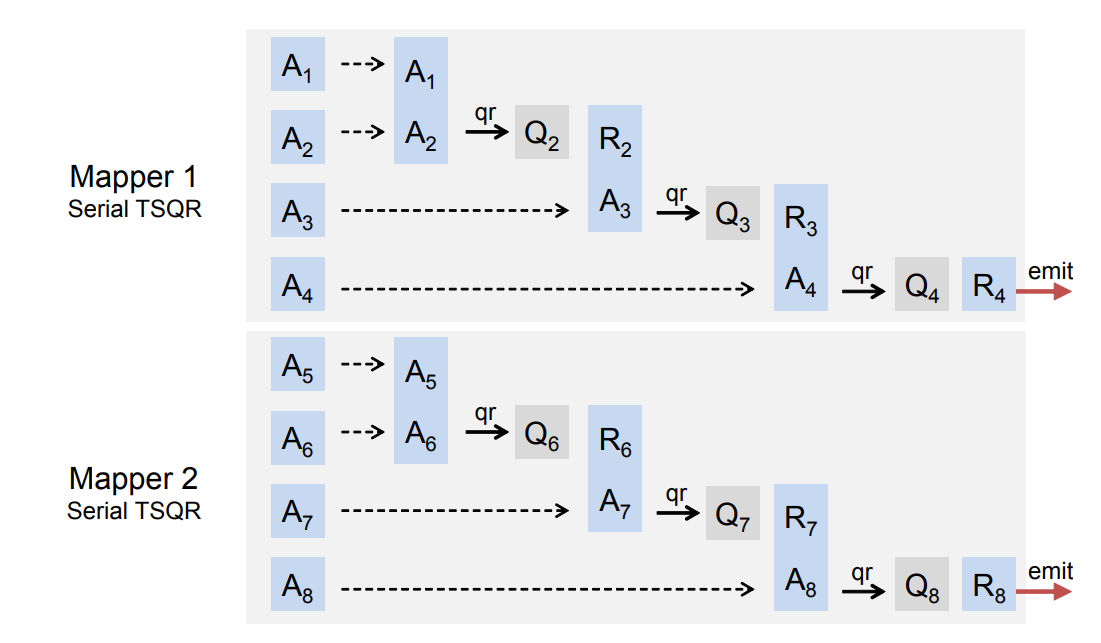
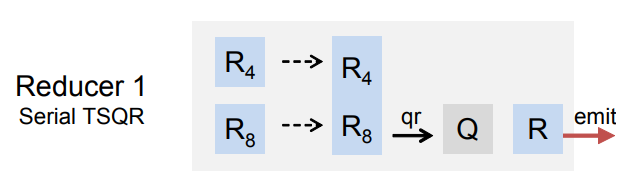
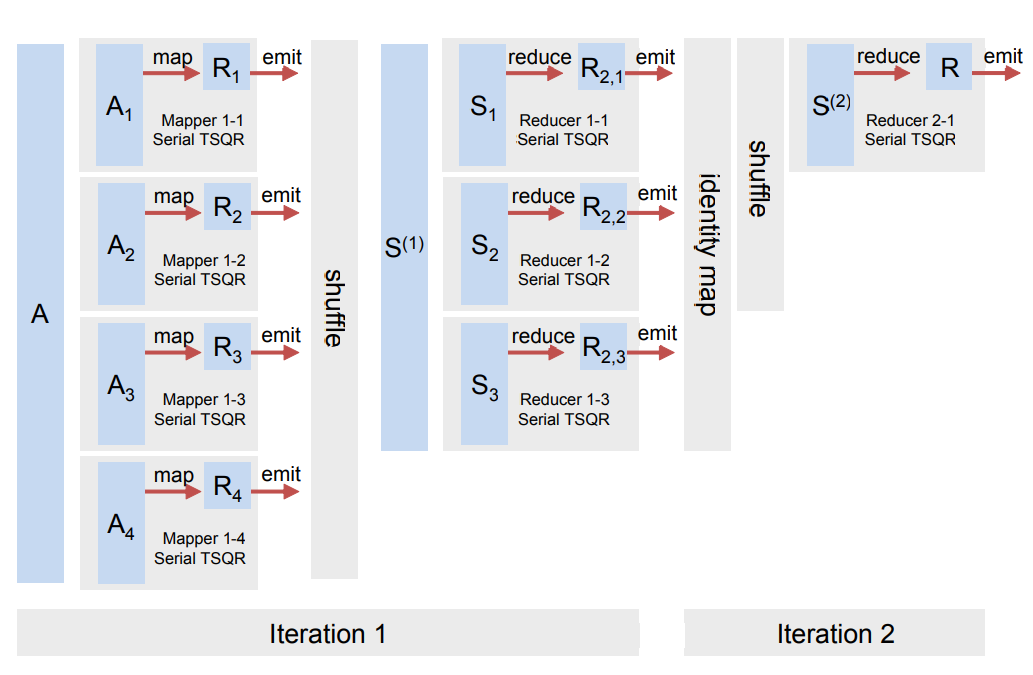
Algorithm

DTQR算法是将 $\R^{m,n}$ 分解成 $Q\in\R^{m,m}$,$R\in\R^{m,n}$，实质上是把下半 $L$ 给变换约去，然后取 $R$ 的上半部分为新的 $R$ ，下图是一个示例。

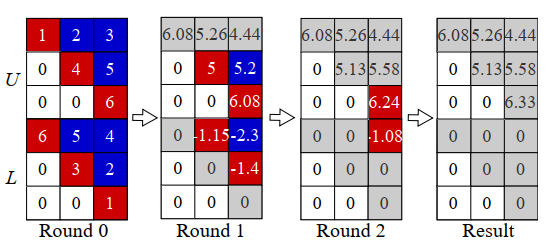
Round0时三行并行Givens运算（givens只改变一行数据），并将L矩阵对角元消除。Round1则两行并行Givens，继续消除L矩阵次对角元。这样形成了逐次远离对角线消元的pipeline顺序，而非Gaussian消元只处理一列。文献[2]提供了HLS如下图的算法（第13行有一定错误，下标少了+n）。

我们定性分析一下性能瓶颈。对于一个大矩阵来说，数据准备绝对是一个瓶颈，如果我们需要等待所有数据完毕，那么将浪费大量时间闲置，所以采用脉动阵列可以有效缓解这个问题。下面的问题是如何布置这个脉动阵列。从上面的算法可以看出，Q和R计算共用了对角元的数据，故可以放在同一列。又因为我们相当于有三个相关任务：计算旋转参数、R计算、Q计算，那么我们都可以在同一列里完成处理。横向则作为每一行的流水运行。

Acceleration Strategy

在[2]的实验部分，作者分析了性能，发现Q矩阵计算成为了新的瓶颈，并且随着矩阵增大而升高。于是，本文则针对Q矩阵的结构设计了新的数据流，提出了Global Acceleration Schemes (GS)和Partially Rotation Skipping (QS)。

GS与文章[2]相同，是上图的优化，将一些没有依赖的行计算并行化。

QS是发现Q矩阵的稀疏性，只需要将非零元素作为Q的存储内容即可。此时在下一个round需要取一列数据的时候，则在这一列没有记录的位置上补上0。如下图，我们需要更新Q矩阵的第二列和第四列，但是我们实际上只存储了四个红色的位置，为了数据排列和处理的统一性，我们补上了蓝色的0，保证两列数据输入时是完整的。同时，我们还可以重用数据到下个round。经过QS的优化，Q旋转矩阵的时间复杂度从普通矩阵乘的$O(n^2)$降到了$O(n)$。（下图Round 0 有点错误，右边蓝框应该右移一列）

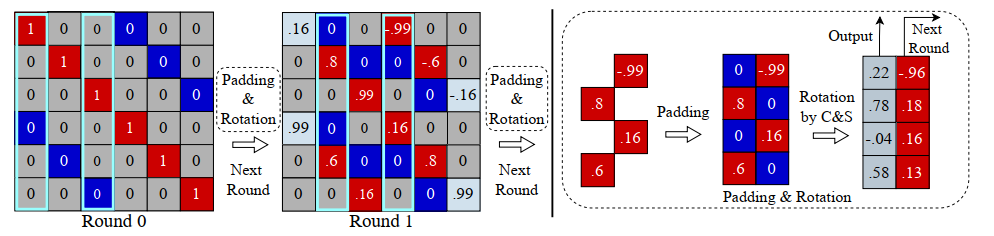
我们还发现，Q的旋转对的指标是不断趋近中心的，不过本文并没有在这方面优化存储。

经过QS优化，在实验部分可以看出，Q计算任务和R计算任务耗时就比较接近了。

Implementation

文章[2]的baseline架构实现如下图。

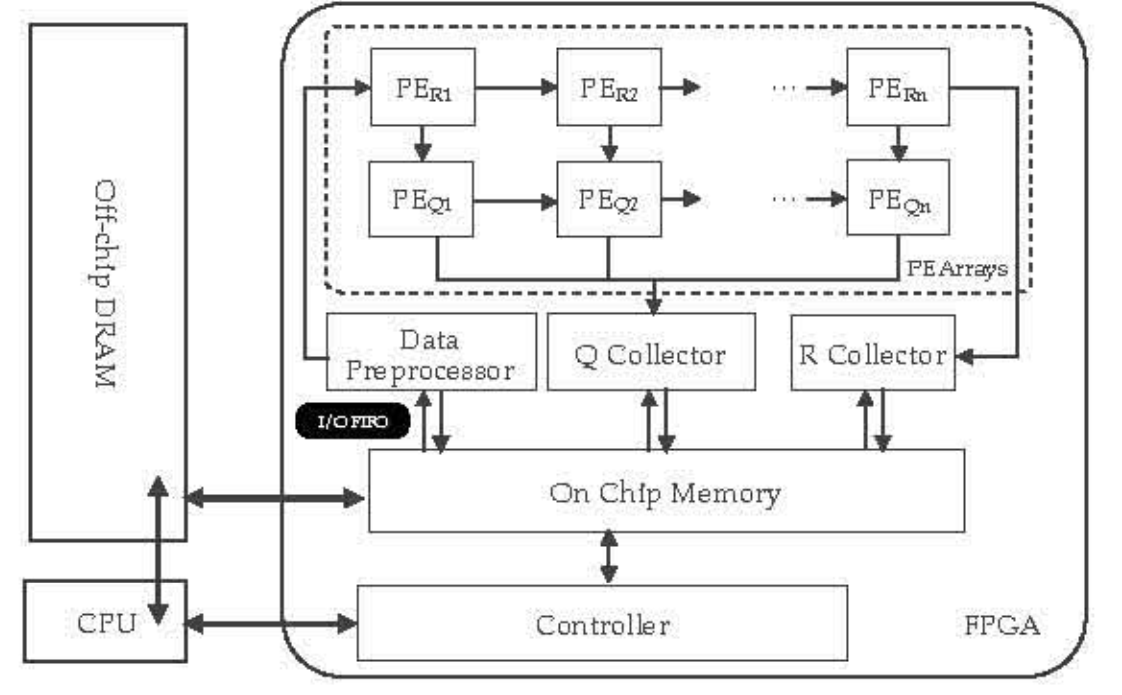
Step1：DMA from DRAM to on-chip BRAM & Data Preprocessing

数据预处理指把对角元数据存在相邻空间中，非对角元数据也可以按所取顺序排列。图中有一个FIFO queue，是指不需要等全部数据都取完就可以开始，后面的数据按顺序进入即可，因为脉动阵列允许异步数据存取。

Step2：Parallel Rotation Parameter Generation & Pipeline Rotation

由于旋转参数计算牵扯到开方和除法运算，运算资源要求远大于R矩阵的旋转部分乘加运算量，若串行则有巨大overhead。并且同一行有多个列的运算，需要在内存中取来大量数据，如果全部同时整块取来，也会在读写方面有overhead。于是，[2]作者提出了Pipeline Rotation，一次只算一行，但是却同时完成下一行的读和上一行的写，分散了同时读写的压力。在行内，采用脉动阵列，完成每一列的计算，保证数据充分复用。

Step3：Task-level Pipeline

前一个Round没结束就接着开始下一个的计算，形成任务之间的重叠。

Step4: Collect

Q collector和R collector作为数据收集器，将矩阵排列好放回Memory，或者继续前递给下一个任务。

在本文中，作者优化了计算部分，改用了1D和2D混合阵列，如下图。

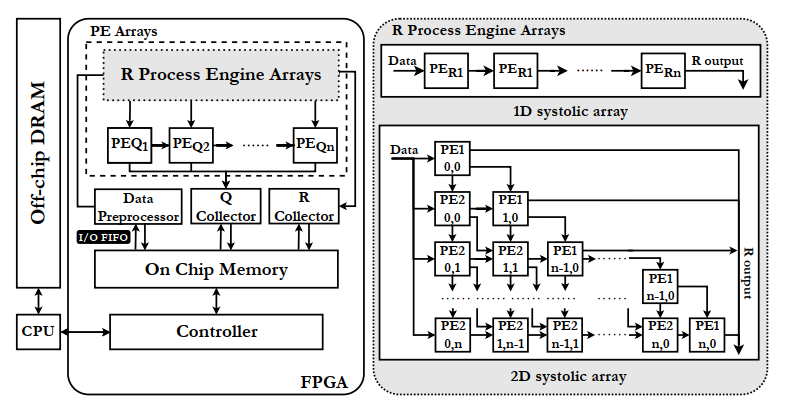
原本的1dPE是需要同时计算旋转参数生成和旋转的，现在将两种功能分离成PE1和PE2，现在PE2可以在没有算出旋转参数之前拿到数据，一旦PE1完成计算就立刻开始，这样一种分离设计减少了闲置的时间，也减少了广播的程度。同时，阵列设计成了统一的三角布置，与R的三角结构对应。（不过感觉1d的阵列里也是这样设计的，或者是更细粒度的pipeline）

Experiment

为了复现相应的微架构，我们先从模拟器复现开始。基于simpy模拟器，可以很容易的模拟事件级的仿真。

系统可以分解成如下的微部件，每个部件之间可以直接相连互相引用，目前正在按层次完成。

verilog仿真将在模拟器验证设计功能之后开始。

实验仍在进行，可以在repo链接里查看具体设计。

Comment

本文已经对QR分解做了很精细的优化了，但可以发现还有些值得改进的点：

• Q矩阵为什么不能用2D PE阵列呢？

可能作者的想法是Q矩阵有较大稀疏性，可以放在一个PE里处理完，再用2D阵列面积撑不住。但是我觉得当n的数量比较大时，这种稀疏性其实是在慢慢消失的，到最后几个PEq非零元素将占大多数，这会对单个PE造成瓶颈，上面的R算完了可能Q还没算完。

因此，我们可以采用1D 和 2D混合处理Q矩阵，即同时兼备面积考虑和效率考虑。

• 已经计算完的行能否提前退出？

从图中我们看到，第一列计算完以后，U矩阵第一行其实已经固定，不需要继续传播，可以直接走快速收集通道离开阵列，减少带宽和负载压力。

同理，Q矩阵也有可以提前退出的列，也可以先行离开。

• R是否也能利用QS优化，比如只记录上三角部分，不用记录下三角？

这个是可以实现的，比如用一些标志信号代表相应行数，免去记录下三角部分。而且我们发现，L矩阵是越来越稀疏的，这样优化也是更好的选择，可以充分利用稀疏性。

• 前递对角元

可以看到，PE2的数据有着列依赖关系，一列的数据必须等待上一列数据计算完毕以后流入，所以这一部分的时间没有办法省去。但是PE1并没有这种关系，既然PE1计算时间是最大瓶颈，为何不把对角元数据先前递到n个PE1里去，减少了大量的冗余处理时间，PE2的数据可以以1clk/col的速度处理，n个clk即可完成处理。

之后，每当前一个任务离开一列，后一个任务就能紧接着进入，提前开始旋转参数计算。

• Data preprocessor优化

按上面所说，我们应该先前递对角元，所以预处理阶段应先行输出对角元到阵列中去，之后可以慢慢收集非对角元数据。

我认为还有些任务级上可以优化的点，更好的把相邻的任务无闲置的衔接，等待上面的idea验证再说。